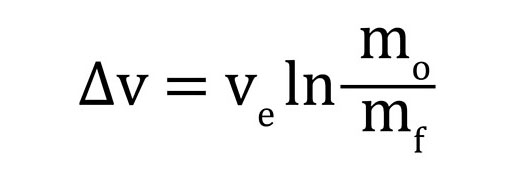Conheça a beleza e elegância da Equação de foguete de Tsiolkovsky
A Equação de Foguete de Tsiolkovsky é uma das demonstrações mais simples e bonitas de como a matemática existe em tudo. Leia e conheça-a.
Carlos Cardoso 3 anos e meio atrás
Um Saturno 5 tem 3 milhões de componentes. São 2.8 mil toneladas e 111 metros de altura. Seus motores produzem potência equivalente a 12 usinas de Itaipu. Mesmo assim ele pode ser descrito perfeitamente com uma equação com apenas 3 parâmetros, a linda Equação de Foguete de Tsiolkovsky.
- Uma Proposta Modesta: O Governo Bolsonaro deveria mandar Israel pro espaço
- DARPA lança desafio pra lançar foguetes em dias ao invés de meses
Antes de chegarmos a ela, precisamos entender como um foguete funciona, e é surpreendentemente simples. Foguetes se movem graças à Terceira Lei de Newton, que determina:
“A toda ação há sempre uma reação oposta e de igual intensidade: as ações mútuas de dois corpos um sobre o outro são sempre iguais e dirigidas em sentidos opostos.”
Por isso inclusive sexo no espaço é algo complicado e vai exigir muito preparo quando forem escrever o NASA Sutra.
O que a 3ª Lei quer diz é que quando você, crossfiteiro está fazendo flexões, você está literalmente empurrando o planeta inteiro, e o planeta te empurra de volta com a mesma força. A menos que você seja kryptoniano essa força é pentelhisimal, claro.
Quando os corpos têm tamanhos relativos mais razoáveis, as forças se fazem sentir melhor.
A 3ª Lei é experimentada no dia-a-dia. Todo mundo (não só a Luma) já viu uma mangueira de bombeiro em ação, e é preciso vários sujeitos pra pressão não jogar todo mundo longe. Um simples balão de ar sai voando quando você deixa o ar escapar pela boca.
Um foguete funciona pelo exato mesmo princípio. Um motor gera uma combustão, que produz gases em extrema pressão. Essa pressão é direcionada pela biqueira do foguete, mas ao mesmo tempo em que a pressão empurra os gases para fora os gases empurram de volta.
A beleza da 3ª Lei de Newton é que funciona com tudo que é matéria, seja sólida, líquida ou gasosa. Ou plasma. Isso nem sempre foi bem entendido.
Nos primórdios da astronáutica vários pioneiros trabalhavam desenvolvendo os princípios que os futuros foguetes usariam. Um deles era Robert Goddard. Ele desenvolveu idéias de foguetes, missões lunares, estações orbitais, etc. Em 12 de Janeiro de 1920 o New York Times publicou um artigo sobre Goddard e suas idéias.
No dia seguinte o mesmo jornal publicou um editorial ridicularizando Goddard. Provando que jornaleiros falando bobagem sobre ciência não são exatamente novidade, o anônimo autor acusou Goddard de desconhecer física básica, pois “no vácuo o foguete não teria contra o quê acelerar”.
Qualquer professor de física de jardim de infância sabe que isso é uma bobagem, mas a idéia se propagou e Goddard foi ridicularizado em vários jornais pelo país. O New York Times só admitiu seu erro em 1969, quando publicou uma errata afirmando que ao contrário do que tinham dito, foguetes podem, sim, se mover no vácuo.
Caímos então em um princípio bem simples: O foguete ejeta os gases da combustão a uma determinada velocidade, isso gera uma força igual em sentido oposto. Quanto maior essa força mais aceleração o foguete ganhará.
Essa força depende da massa dos gases ejetados e da velocidade com que eles são expelidos. Isso é fundamental, por isso se eu empurrar uma bigorna contra você, você nem vai perceber, mas se eu deixar a bigorna cair do 178º andar, vai doer, no mínimo deixar marca.
Segundo Newton e Tsiolkovsky, quanto mais massa e mais rápido o foguete ejeta, mais ele acelera. Por isso foguetes são mais de 95% combustível.
A Equação de Tsiolkovsky
Aqui entra o pulo do gato: Quando você está queimando combustível em um foguete, a massa total diminui, se você queima uma tonelada por segundo, seu foguete fica uma tonelada mais leve a cada segundo, então o combustível queimado tem menos foguete para empurrar, tornando o processo mais eficiente.
A Equação de Tsiolkovsky calcula quanta velocidade você consegue adicionar ou subtrair de um foguete, levando em conta a massa total, a massa do combustível queimado e a velocidade de exaustão dos gases.
Todo o resto não importa. Não interessa se é um motor nuclear NERVA, um foguete de pólvora, um motor iônico ou o Falcon Heavy. A equação só não funciona pro VLS porque ele explode antes.
A equação foi derivada independentemente por vários cientistas, como Robert Goddard (1912), Herman Oberth (1920) William Moore (1810) e William Leitch (1861), mas foi o russo Konstantin Tsiolkovksy quem primeiro aplicou a equação explicitamente a foguetes e trajetórias orbitais, em 1903, por isso ele é o pai oficial e ela foi batizada em sua homenagem.
A equação que calcula o Delta-V (ΔV), a variação de velocidade do foguete se resume a isto:
Aonde:
ΔV é a variação de velocidade
Ve é a velocidade de exaustão a biqueira do foguete.
Mo é a massa inicial do foguete
Mf é a massa final, menos o combustível queimado.
Aplicando a conta, um foguete usando um motor Raptor da SpaceX, pesando 500 toneladas, dessas 480 sendo combustível teria um ΔV de 11.91Km/s. É preciso pelo menos 8Km/s para entrar em órbita.
Claro que na prática há várias perdas, a pressão na câmara de combustão não é a mesma em todos os eixos e o próprio ar atrapalha no começo do lançamento. Isso mesmo, para tristeza do jornaleiro do New York Times não só foguetes não precisam de ar para funcionar, como atmosfera densa os torna menos eficientes, o ar atrapalha os gases ejetados, exercendo resistência.
Existem algumas alternativas para conseguir mais ΔV. Uma delas é levar mais combustível, mas aí caímos em um problema: Mais combustível aumenta a massa total do foguete.
Outra solução é aumentar a velocidade com que os gases são ejetados. Na mesma SpaceX o primeiro motor Merlin, usado no Falcon 9 tinha uma velocidade de exaustão de 3050 metros por segundo.
Nosso hipotético foguete de 500 toneladas com 480t de combustível usando um Merlin conseguiria um ΔV de 9.818 km/s, segundo Tsiolkovsky.
Já se trocarmos o Merlin por um Raptor, com velocidade de exaustão de 3700m/s o ΔV sobe para 11.91km/s.
Motores iônicos
Hoje em dia todo satélite que se preza usa motores iônicos, capazes de acelerar quantidades diminutas de propelente a uma velocidade muito grande, por muito tempo. Não é uma reação de combustão, partículas ionizadas, geralmente núcleos de Xenônio são aceleradas por campos elétricos, e a velocidade de exaustão pode chegar a 50000m/s.
Nosso hipotético foguete usando um motor iônico teria um ΔV de 160.94Km/s. Dá pra ir pra qualquer lugar do sistema solar com isso.
Só Não dá pra sair do chão, motores iônicos exercem uma aceleração muito pequena durante muito tempo, que na soma chegam ao incrível ΔV acima.
A Equação de Tsiolkovsky e o Futuro
Enquanto alguém não descobrir novas Leis da Física ainda vamos depender de ação e reação, nossas futuras naves continuarão tendo que ejetar massa para acelerar. Em The Expanse o Sistema Solar foi conquistado graças ao Motor Epstein, um equipamento extremamente eficiente que consegue um ΔV imenso mesmo as naves sendo pequenas, ou seja: Elas levam pouco combustível.
Quem tem aquário em casa já deduzir a solução lógica: Eles aceleram o plasma ejetado. Mas será possível algo assim?
Peguemos a Rocinante, de Expanse. É uma corveta modificada com massa de 2400 toneladas. Imaginemos que 100 toneladas são combustível. Segundo a Equação de Tsiolkovsky, com a mesma eficiência de um motor Raptor da SpaceX ela conseguiria um ΔV de 0.15Km/s.
Com a velocidade de exaustão de um motor iônico, esse ΔV sobe para 2.12Km/s.
E se aumentarmos essa velocidade de exaustão para 1.000.000m/s? O ΔV agora é de 42.56km/s.
Uma velocidade de exaustão de 10.000.000km/h colocaria a Rocinante com um ΔV de 118.22Km/s. Dez milhões de Km/h parece muito, mas é apenas 0,0092 da velocidade da luz.
O Large Hadron Collider consegue acelerar feixes de partículas a 99.9999991% da velocidade da luz.
Imaginemos que a Rocinante tem um reator de fusão nuclear (expectativa de uso comercial em 20 anos) imensamente eficiente gerando quantidades imensas de energia. Essa energia é usada em um motor que acelera a matéria ejetada a 100.000.000km/h, ou 10% da velocidade da luz. O ΔV agora é de 1182.2Km/s.
Com esse ΔV não é mais preciso seguir órbitas de baixa energia, dá para viajar de planeta para planeta praticamente em linha reta, chegando a Marte em questão de dias, a limitação é a capacidade humana de resistir à aceleração.
Em um cenário ideal a nave aceleraria a 1g até metade do caminho, viraria 180º e começaria a desacelerar na mesma taxa, proporcionando um ambiente com gravidade normal (para nós, não pros malditos belters). No nosso foguete hipotético acima, a viagem entre Terra e Marte, a uma distância de 69.7 milhões de Km levaria... 32 horas.
Saindo hoje com foguetes atuais leva 11 meses.
Ninguém faz idéia de como conseguir essas velocidades, acelerar matéria a uma fração considerável da velocidade da luz é algo que exige imensa quantidade de energia e nunca foi feito com uma quantidade considerável de matéria. Mesmo assim, quando decifrarmos esse enigma da engenharia e conseguirmos construir naves com motores ejetando plasma a 10%, 20% ou mesmo 50% da velocidade da luz, provavelmente pessoas do Século XX sequer conseguiriam reconhecer a ciência envolvida, afinal qualquer tecnologia suficientemente avançada é indistinguível de magia.
O que continuará funcionando é uma simples equação: Delta-V é igual à velocidade de exaustão multiplicada pelo logaritmo natural da divisão entre a massa inicial e a massa final, fruto de Konstantin Tsiolkovsky, um homem que sonhou com foguetes antes do avião ser inventado.