MIT apresenta novo algoritmo 10x mais rápido que o FFT atual
No começo dessa semana o MIT apresentou durante simpósio um novo algoritmo capaz de amplificar e melhorar substancialmente o desempenho prático da FFT.
FFT, ou Fast Fourier Transform, é o algoritmo mais prevalente em todas as ciências da comunicação e tem sido empregado sem descanso em quase tudo o que conhecemos desde quando foi composto, em meados dos anos 1960. Sem ele não seria possível, por exemplo, converter informações como notas musicais e outros dados puros na forma de uma representação matemática que pudesse ser codificada e transmitida entre dispositivos.
O FFT é uma composição matemática que decompõe a matriz de um sinal qualquer em amplas frequências, complexas e específicas o bastante para obedecerem a um padrão de leitura e codificação. Sem ele não seria possível entender as flutuações de voltagem de um fio que conecta um arquivo de .mp3 dentro de um player a uma caixa de som. Ou seja, precisamos dele.
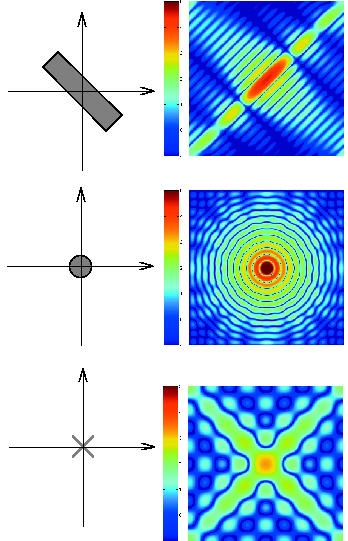
Tal qual seu predecessor, o novo algoritmo também opera com sinais digitais em um espectro complexo de frequências com diferentes ondulações e que representam valores distintos.
Um bloco de 8×8 pixels pode ser entendido como um sinal contendo 64 amostras frequenciais e, portanto, a soma destas 64 diferentes frequências se considerarmos a escala de Transformação de Fourier.
Muitas dessas 64 frequências têm latência tão baixa que podem ser desconsideradas. Por esta razão a FFT é tão importante para a compressão de dados.
O que os professores Katabi e Piotr Indyk do Laboratório de Inteligência Artifical e Ciência da Computação (CSAIL) do MIT descobriram é que na verdade 57 destas frequências podem ser completamente ignoradas sem perdas significativas de qualidade — o que aumenta em pelo menos 10 vezes a velocidade do novo algoritmo.
Ainda sem nome, ele pode ser especialmente útil para smartphones e tablets, oferecendo a possibilidade de conversão e transmissão de longos arquivos de vídeo, sem que se drenem suas baterias ou se consuma excessivamente as suas respectivas franquias de dados oferecidas pelas operadoras.
O seu desenvolvimento contou com a ajuda dos alunos Eric Price e Haitham Hassanieh e consiste de uma nova ideia em relação ao método atual, dividida em dois passos: o primeiro é dividir e mensurar o sinal em camadas mais estreitas de banda, de modo que cada camada contenha apenas uma única frequência com ‘peso’ de marcação significativo e seja assim considerada, descartando-se as demais.
Com informações: MIT News e MathWorks.
